用整数规划求解三维装箱问题

背景

在电商业务中，一个核心的生产环节是 打包：把用户购买的商品打包装入纸箱。

纸箱成本一般与纸板面积成正比。为了节约打包成本，我们希望从候选纸箱中选择 最小的 纸箱来装用户购买的商品。在实际操作中，工人一般倾向于选择较大的纸箱，不仅能减少选择纸箱的时间，而且能降低装箱难度，从而加快生产效率。但这样做会显著增加生产成本。为了节约成产成本，我们考虑用算法来指导工人选择最合适的箱型。

装箱问题

从算法角度解决上述问题有如下难点：

1. 商品的形状不规则：有些商品没有外包装, 例如啤酒瓶是圆柱状, 而垃圾桶是中空的。
2. 商品的材质软硬不同：毛巾，衣服等商品可以折叠，那么如何测量其几何形状? 装箱时是否可以折叠?
3. 商品的摆放方式自由：在业务允许的前提下，商品可以旋转，倾斜，折叠等方式进行摆放。
4. 判定纸箱是否能装下商品：给定商品信息和纸箱三维长度，如何判定商品能否装下?

因此，需要把问题适当简化。我们做如下假设：

1. 把每个商品看成长方体，并测量其长宽高。
2. 不考虑可以折叠和中空的商品。
3. 所有商品能够以 90° 旋转。

剩下的问题是如何用算法来判定给定的商品是否能装入给定的纸箱。如果这个问题得到解决，我们就可以对每个纸箱求解一次该问题, 从而选择能装下所有商品的最小箱子。

从计算复杂性的角度来，该问题属于NP-complete¹。在 NP $\neq$ P 的假设下²，该问题不能在多项式时间内求解。换句话说，我们找不到"又快又好"的算法求解该问题。在实际中，我们经常采用效率换质量的策略来求解这一类问题。即，允许算法不是最优解，但要求在可以接受的时间内返回可行解(feasible solution)。

这样一来可能出现算法推荐不正确的问题：

1. 推大用小：算法推荐的纸箱比工人实际使用的纸箱大。在这种情况下，工人的操作会比算法推荐更节约成本.
2. 推小用大：算法推荐的纸箱比工人实际使用的纸箱小。在这种情况下，工人的操作会失败，不仅会误导工人，而且降低生产效率。

因此, 算法要避免产生推小用大的错误。换句话说，算法推荐的纸箱一定要能装下所有商品。

启发式算法

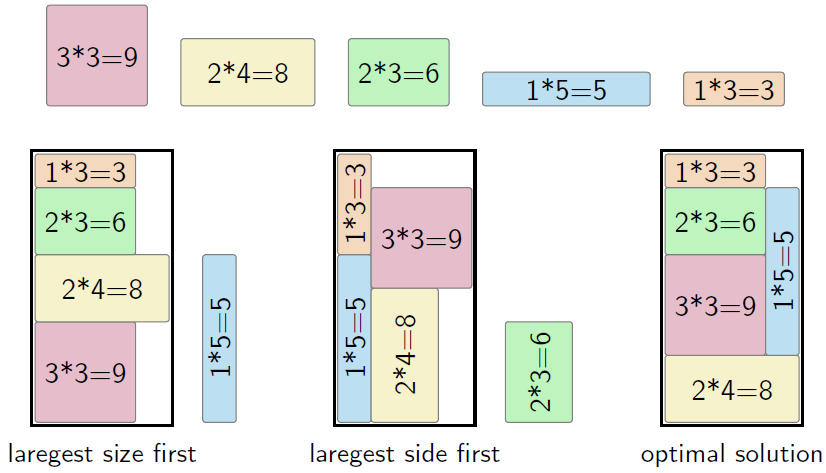
比较容易想到的是设计一些装箱的规则，例如最大体积优先，最大面积优先等，其缺点是我们无法保证得到最优解。我们以二维装箱为例，下图的例子考虑 5 个商品，方块中的数字代表长 $\times$ 宽，箱子的大小为 $8\times 4$。最大面积优先 和 最长边优先 的装箱策略均无法得到最优解。

整数线性规划

下面介绍一种求最优解的方法。基本思想是把该问题用数学语言来描述，从而建立优化目标和不等式组。利用数学规划求解器来解对应的数学问题，从而得到最优解。难点在于如何建立该问题的数学模型³。

下标

为方便描述，我们用下标 $i，j$ 代表商品，$k$ 代表商品摆放方式。

• $i, j \in {1, 2, \ldots, n}$ – 商品
• $k \in {1, 2, \ldots, 6 }$ – 商品的摆放方式(对应 $\sigma_k$)

输入参数

• $n$ – 商品数量
• $L, W, H$ – 箱子的长宽高
• $l_i, w_i, h_i$ – 商品 $i$ 的长宽高

决策变量

给定长方体 $(L, W, H)$ (代表商品或纸箱)，用如图所示的左手坐标系，把长方体置于原点(使得长方体中所有点的坐标非负)。 因此，任意一个长方体可以用图中的 $a, b$ 两点来确定位置。我们把 $a$ 点称为长方体的位置。

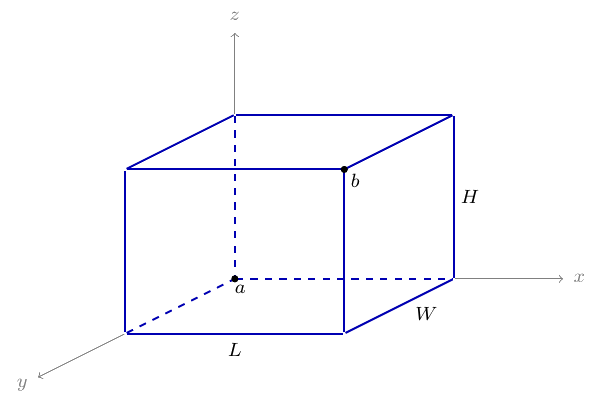
定义商品的 $a$ 点和 $b$ 点坐标：

• $x_i \in [0, L], y_i \in [0, W], z_i \in [0, H]$ – 商品 $i$ 的位置坐标(即 $a$ 点坐标)
• $\hat{l}_i \in [0, L], \hat{w}_i \in [0, W], \hat{h}_i \in [0, H]$ – 商品 $i$ 的 $b$ 点坐标

如图所示, 上述长方体的位置为 $(0,0,0)$, $b$ 点坐标为 $(L, W, H)$。允许90°旋转的条件下，它一共有6种摆放方式，即$(L, W, H)$ 的所有置换(Permutation)： $$ \sigma_1: \quad (L, W, H) \\ \sigma_2: \quad (L, H, W) \\ \sigma_3: \quad (W, L, H) \\ \sigma_4: \quad (W, H, L) \\ \sigma_5: \quad (H, L, W) \\ \sigma_6: \quad (H, W, L) $$

$k=1,2,\ldots, 6$ 表示按上述第 $k$ 种摆放方式 $\sigma_k$。用 $\delta_{ik}$ 来表示商品 $i$ 是否按照第 $k$ 种方式摆放。

• $\delta_{ik} \in {0, 1 }$ – 商品 $i$ 按第$k$种方式摆放。

考虑任意两个商品$i, j$。它们一共有 6 种相对位置：

• $a_{ij}$ – $i$ 在 $j$ 的左侧

• $b_{ij}$ – $i$ 在 $j$ 的右侧

• $c_{ij}$ – $i$ 在 $j$ 的后面

• $d_{ij}$ – $i$ 在 $j$ 的前面

• $e_{ij}$ – $i$ 在 $j$ 的下面

• $f_{ij}$ – $i$ 在 $j$ 的上面

• $a_{ij}, b_{ij}, c_{ij}, d_{ij}, e_{ij}, f_{ij} \in { 0,1 }$ – 商品 $i$ 和 $j$ 的 6 种位置关系

约束条件

下面我们建立 $(l_i,w_i,h_i)$ 与 $(\hat{l}_i, \hat{w}_i, \hat{h}_i)$ 之间的对应关系。回顾 $\delta_{ik}$ 代表商品 $i$ 的第 $k$ 种摆放方式，我们有 $$ \hat{l}_i = \delta_{i1}l_i + \delta_{i2}l_i + \delta_{i3}w_i + \delta_{i4}w_i + \delta_{i5}h_i + \delta_{i6}h_i\\ \hat{w}_i = \delta_{i1}w_i + \delta_{i2}h_i + \delta_{i3}l_i + \delta_{i4}h_i + \delta_{i5}l_i + \delta_{i6}w_i\\ \hat{h}_i = \delta_{i1}h_i + \delta_{i2}w_i + \delta_{i3}h_i + \delta_{i4}l_i + \delta_{i5}w_i + \delta_{i6}l_i $$

注意到商品 $i$ 不能同时存在两种摆放方式，因此 $$\sum_{k=1}^6\delta_{ik} = 1.$$

考虑任意两个商品$i,j$，它们之间有 6 种位置关系：$i$ 在 $j$ 的左侧，右侧，后面，前面，下面，上面。分别用 $a_{ij}, b_{ij}, c_{ij}, d_{ij}, e_{ij}, f_{ij}$ 表示。 回顾商品 $i$ 的位置坐标为 $(x_i,y_i,z_i)$。以 $i$ 在 $j$ 的左侧为例，即，当 $a_{ij}=1$ 时，我们有 $x_i + \hat{l}_i \leq x_j$。如图所示。

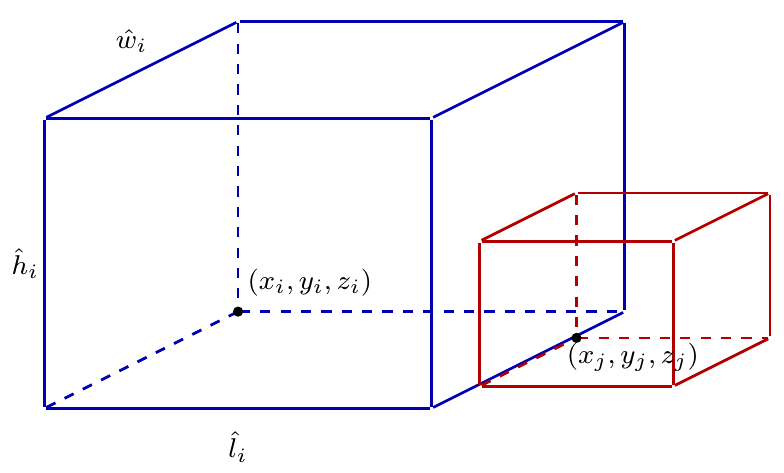
类似地，我们有

• $a_{ij} = 1 \Rightarrow x_i + \hat{l_i} \leq x_j$
• $b_{ij} = 1 \Rightarrow x_j + \hat{l_j} \leq x_i$
• $c_{ij} = 1 \Rightarrow y_i + \hat{w_i} \leq y_j$
• $d_{ij} = 1 \Rightarrow y_j + \hat{w_j} \leq y_i$
• $e_{ij} = 1 \Rightarrow z_i + \hat{h_i} \leq z_j$
• $f_{ij} = 1 \Rightarrow z_j + \hat{h_j} \leq z_i$

把上述关系写成不等式, 我们得到

$$ \begin{aligned} & x_i+\hat{l_i}\le x_j +(1-a_{ij})L \\ & x_j + \hat{l_j}\le x_i +(1-b_{ij})L \\ & y_i +\hat{w_i}\le y_j +(1-c_{ij})W \\ & y_j +\hat{w_j}\le y_i +(1-d_{ij})W \\ & z_i +\hat{h_i}\le z_j + (1-e_{ij})H \\ & z_j +\hat{h_j}\le z_i + (1-f_{ij})H \end{aligned} $$

在上述 6 种相对位置中，(左, 右)，(前, 后)，(上, 下) 每一对关系不能同时存在，因此

$$ \begin{aligned} & a_{ij} + b_{ij} \leq 1\\ & c_{ij} + d_{ij} \leq 1\\ & e_{ij} + f_{ij} \leq 1 \end{aligned} $$

但是, 这 6 种相对位置至少有一种必须存在。我们有 $$a_{ij} + b_{ij} + c_{ij} + d_{ij} + e_{ij} + f_{ij} \geq 1.$$

已知商品 $i$ 的位置是 $(x_i, y_i, z_i)$，它的 $b$ 点坐标为 $$(x_i+\hat{l}_i, y_i+\hat{w}_i, z_i + \hat{z}_i).$$

由于装入纸箱的商品不能超过纸箱的长宽高，因此 $$ \begin{aligned} & x_i + \hat{l}_i \leq L\\ & y_i + \hat{w}_i \leq W\\ & z_i + \hat{h}_i \leq H \end{aligned} $$

数学模型

综上所述，我们得到如下的数学规划问题。 $$ \begin{aligned} \min ~ & 0 \\ \text{s.t. } & a_{ij} + b_{ij}\le 1, \quad \forall i<j \\ &c_{ij}+d_{ij}\le 1, \quad \forall i<j\\ &e_{ij}+f_{ij}\le 1, \quad \forall i<j \\ &a_{ij}+b_{ij}+c_{ij}+d_{ij}+e_{ij}+f_{ij}\ge 1, \quad \forall i<j\\ &\sum_{k=1}^6\delta_{ik}=1,\quad \forall i\\ &\hat{l}_i = \delta_{i1}l_i +\delta_{i2}l_i +\delta_{i3}w_i +\delta_{i4}w_i +\delta_{i5}h_i +\delta_{i6}h_i, \quad \forall i\\ &\hat{w}_i = \delta_{i1}w_i +\delta_{i2}h_i +\delta_{i3}l_i +\delta_{i4}h_i +\delta_{i5}l_i +\delta_{i6}w_i, \quad \forall i\\ &\hat{h}_i = \delta_{i1}h_i +\delta_{i2}w_i +\delta_{i3}h_i +\delta_{i4}l_i +\delta_{i5}w_i +\delta_{i6}l_i, \quad \forall i\\ & x_i+\hat{l}_i\le x_j +(1-a_{ij})L, \quad \forall i<j\\ & x_j + \hat{l}_j\le x_i +(1-b_{ij})L, \quad \forall i<j\\ & y_i +\hat{w}_i\le y_j +(1-c_{ij})W, \quad \forall i<j\\ & y_j +\hat{w}_j\le y_i +(1-d_{ij})W, \quad \forall i<j\\ & z_i +\hat{h}_i\le z_j + (1-e_{ij})H, \quad \forall i<j\\ & z_j +\hat{h}_j\le z_i + (1-f_{ij})H, \quad \forall i<j\\ & x_i+\hat{l}_i\le L, \quad \forall i\\ & y_i+\hat{w}_i\le W, \quad \forall i\\ & z_i+\hat{h}_i\le H, \quad \forall i\\ & \delta_{ik},a_{ij},b_{ij},c_{ij},d_{ij},e_{ij},f_{ij}\in {0,1}, \quad \forall i < j, \forall k\\ & x_i,y_i,z_i\ge 0, \quad \forall i \end{aligned} $$

利用开源工具 OR-Tools 或商用求解器 (例如Gurobi) 求解上述问题，如果有可行解则表示纸箱能装入所有商品。

说明 该精确算法的计算时间随商品数量成指数增长。因此仅限于求解小规模问题，例如商品数量限定在 10 个以内。在实际应用中，小规模问题我们可以使用精确算法，而大规模问题可以考虑启发式算法。

参考文献