三维装箱问题的搜索树算法

考虑如下问题：

• 输入: 长宽高为 $(L, W, H)$ 的箱子和 $n$ 个物品，其长宽高为 $(l_i, w_i, h_i)$, $i=1,2,\ldots,n$。假设物品是长方体，长度不可变(没有弹性)。装箱时可以对商品进行 90 度旋转，但不能倾斜。
• 输出: 判断所有物品是否能装入箱子。

本文提供一个基于搜索树的精确算法。基本思想是把三维装箱问题归约 (Reduce) 到一个有向无环图 (Directed Acyclic Graph) 上的问题。算法搜索到一个符合约束条件的有向无环图则返回 true, 否则返回false。

物品的位置

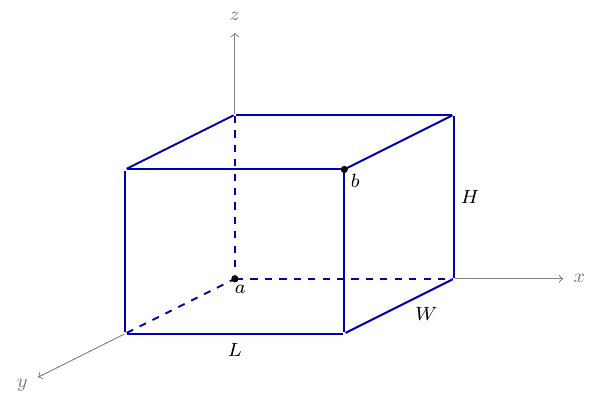
如下图所示，考虑任意一个物品 (或者箱子)，我们可以用 $a$, $b$ 两点的三维坐标描述其位置和大小。设 $a=(x_a,y_a,z_a)$，那么 $b=(x_a+L, y_a+W, z_a+H)$，其中 $L, W, H$ 是物品的长宽高。为了方便描述，我们用 $a$ 点的坐标表示物品的位置。

有向无环图

假设所有物品能够被装入箱子中。此时我们考虑一种可行的摆放方式。对两个物品 $i \neq j$, 分别考虑 $x, y, z$ 轴方向物品之间的相对位置关系。

首先考虑 $x$ 轴方向, $i$ 和 $j$ 只有两种位置关系

1. $i$ 在 $j$ 的左边，即 $x_i \leq x_j$，其中 $x_i, x_j$ 为物品在 $x$ 轴的坐标；
2. $i$ 在 $j$ 的右边，即 $x_i > x_j$。

下面我们构造有向图 $D_x = (V, u^x, A_x)$。其中

• $V={1, 2, \ldots, n}$是所有物品的集合。
• $u^x$ 为顶点权重的集合, 即 $u^x_i=l_i$，$\forall i=1, 2, \ldots, n$。
• $A_x$ 为弧(Arc)的集合。如果 $i$ 在 $j$ 的左边，则 $(i, j)\in A_x$，否则 $(j,i)\in A_x$ (如下图所示)。 注意: 如果 $(i, j), (j,k) \in A_x$，则 $(i,k)\in A_x$。换句话说，$D_x$ 无环。

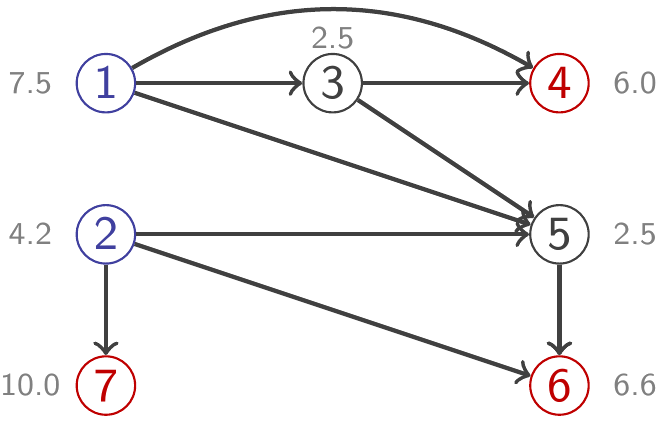
令 $S_x, T_x$ 分别代表 $D_x$ 中的 入度(in-degree) 为 0 和 出度(out-degree) 为 0 的点集。以上图为例，$S_x = \set{1, 2}$ (蓝色的点)，$T_x=\set{4, 6, 7}$ (红色的点)。对任意的 $s\in S_x$，$t\in T_x$，用 $P^x_{s,t}$ 代表从 $s$ 到 $t$ 的路径。令 $u(P^x_{s,t})$ 代表 $P^x_{s,t}$ 中顶点的总权重，即

$$u(P^x_{s, t}) = \sum_{i\in P^x_{s,t}}{u^x_i} = \sum_{i\in P^x_{s,t}}{l_i}.$$

考虑到装入箱子的物品总长度不能超过箱子的长，我们要求

$$\max_{s\in S_x, t\in T_x} u(P^x_{s, t}) \leq L.$$

用类似的方法考虑 $y$ 轴和 $z$ 轴方向并构造 $D_y=(V, u^y, A_y)$ 和 $D_z=(V,u^z, A_z)$，其中

• $u^y_i=w_i$，$u^z_i=h_i$, $i=1, 2, \ldots, n$。
• $(i, j) \in A_y$表示$i$在$j$的后方(反之$i$在$j$的前方)。
• $(i, j) \in A_z$表示$i$在$j$的下方(反之$i$在$j$的上方)。

下面我们得到所有物品能装入箱子的充要条件：

1. $G=(V, E(A_x\cup A_y \cup A_z))$ 是一个团(Clique)，其中记号$E(A)$代表有向边集合$A$对应的无向边集合。
2. $\max_{s\in S_x, t\in T_x} u(P^x_{s, t}) \leq L$。
3. $\max_{s\in S_y, t\in T_y} u(P^y_{s, t}) \leq W$。
4. $\max_{s\in S_z, t\in T_z} u(P^z_{s, t}) \leq H$。

搜索策略

结合前文的讨论, 我们先总结分支的因素:

• 需要比较任意两个物品之间的相对位置, 共有$C_n^2$种情况.
• 两个物品之间共有6种相对位置关系: 左右, 后前, 下上.
• 每种物品最多有6种不同的摆放方式: $(l, w, h), (l, h, w), (w, l, h), (w, h, l), (h, l, w), (h, w, l)$.

用 $I_k (1\leq k \leq n)$ 表示一个装箱问题的实例, 其中物品集合为 ${1, 2, \ldots, k}$。我们搜索的策略是用深度优先的方式依次判断 $I_1, I_2, \ldots, I_n$ 的可行性。设 $I_k$ 可行。

考虑$I_{k+1}$ 时, 我们需要对比 $(1, k+1), (2, k+1), \ldots, (k, k+1)$。此外，对每个物品对(pair) $(i, k+1)$，$1\leq i\leq k$，我们要考虑 $6\times 6 = 36$ 种相对位置和排放方式。因此, 对 $I_k$ 的任意一搜索节点，它的分支数量是 $36k$ (示意图如下)。

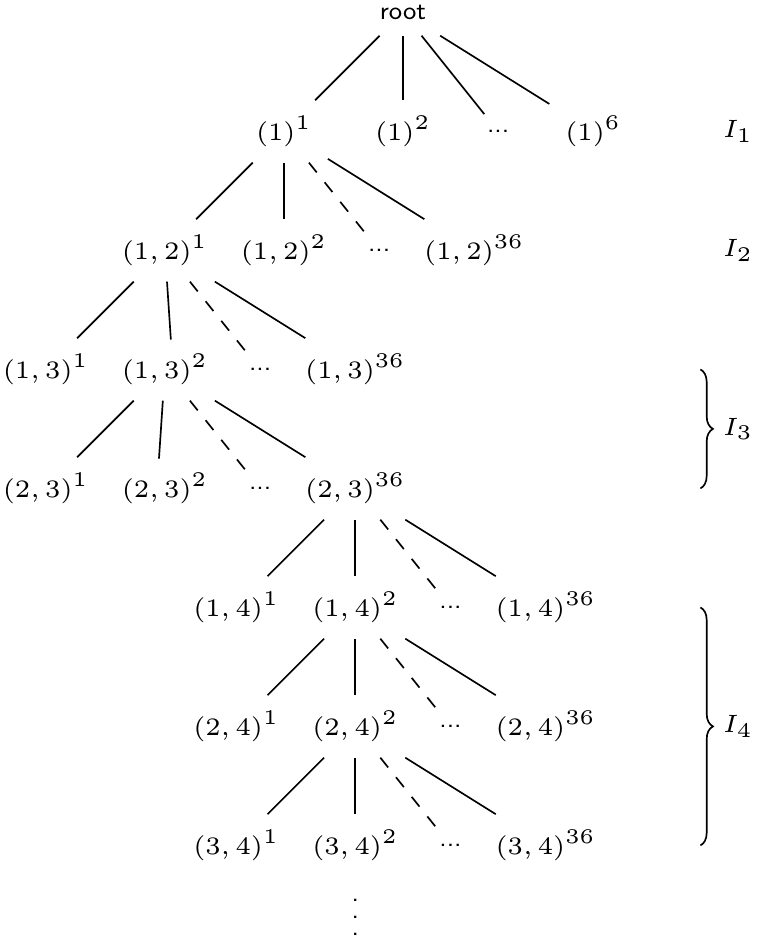
说明：从根节点root开始搜索。第一层是判断 $I_1$ 是否可行，由于 $I_1$ 包含 1 个物品，因此只需要考虑 6 种摆放方式，即 $(1)^1, \ldots, (1)^6$；第二层判断 $I_2$ 是否可行，需要比较两个物品 $(1, 2)$，其中每个节点有 36 个分支，对应 6 种相对位置关系和物品2的六种摆放方式的组合；第三，四层判断 $I_3$ 是否可行，需要比较 $(1,3)$ 和 $(2,3)$；依此类推。

注意：分支前必须检查两个物品间是否已经有位置关系，若有，则当前节点不需要分支(确保无环)。例如，如果物品 1 在物品 2 的左边，物品 2 在物品 3 的左边，那么物品 1 一定在物品 3 的左边，因此无需比较物品 3 在物品 1 左边的情况。

优化策略

1. 物品的排序比较重要。直观的做法是把物品按照体积由大到小排序。
2. 物品的摆放方式实际上是 1-6 种。如果物品是立方体，则只需要考虑 1 种摆放方式。在实际中应该额外考虑三边相同和两边相同的情况。
3. 判定 $I_2$ 时可以考虑物品的对称性，因此相对位置只要考虑左，后，下。
4. 比较物品间的相对位置时按照"从外到内"的原则，即右，前，上，左，后，下。

可行性判定

考虑三维装箱实例 $I_k$，$1\leq k\leq n$。令 $D^k_x, D^k_y, D^k_z$ 为 $x,y,z$ 轴方向的有向无环图。令 $D^k=(D^k_x, D^k_y, D^k_z)$。如上图所示，我们的搜索过程需要判断 $D^1, D^2, \ldots, D^n$的可行性。考虑 $D^k$: 顶点个数是 $3k$，边的个数是 $O(k^2)$，因此 最长路(顶点权重之和最大) 的计算可以在 $O(k^2)$ 的时间内完成。具体来说，以 $D^k_x$ 为例，我们可以维护每个顶点 $i(1\leq i\leq k)$ 的最长路程。当考虑 $D^{k+1}_x$ 时，例如增加弧 $(i, k+1)$ 或 $(k+1, i)$，我们只需要更新 $k+1$ 所有子节点的最长路程即可。

时间复杂度

搜索树第 $k$ 层 (root 是第 0 层) 对应的节点数量是 $36^{k-1}$。如上图所示，实例 $I_k(\geq 2)$ 包含了 $k-1$ 层。因此，从第二层到叶子节点一共有 $n(n-1)/2$ 层。因此，搜索树的节点总数 $N$ 为： $$N = \sum_{k=1}^{n(n-1)/2} 36^{k-1} + 7 = O(6^{n^2}).$$ 每个节点判断可行性的时间为 $O(n^2)$，因此算法的时间复杂度为 $O(6^{n^2}\cdot n^2)$。