用 Prophet 做时间序列预测
目录
电商的业务场景中有很多决策依赖预测模型的输入,其中时间序列预测是一类比较基础的模型,服务于采购、营销、仓配、客服等业务。本篇介绍开源时序预测框架Prophet的基本原理和使用方法。
1. 简介
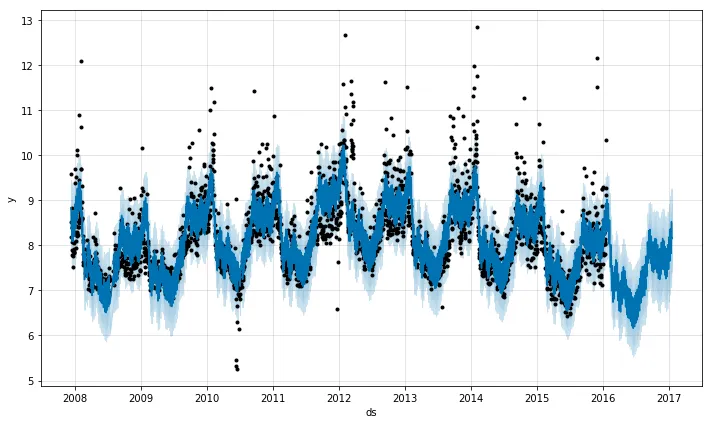
Prophet[1]是 Facebook 在2017年开源的时间序列预测算法,提供了 R 和 Python 语言的支持[2]。Prophet非常容易上手,短短几行代码就能建立时序预测模型,算法的基本思想类似于时间序列分解,将时间序列分成为趋势(Trend),季节性(seasonality)和节日(holiday)。
Prophet能自动识别一些简单周期(年/周/日),并内置了节假日模块,甚至支持了中国节日(包括农历节日,如端午节、中秋节)。此外,它还能自动剔除异常值和处理缺失值。
Prophet提供了大量可配置的参数,使用者可根据具体需求调整模型,比如调整季节性的拟合度,添加自定义节假日,添加自定义变量等。不同的参数配置可能得到完全不一样的模型,所以使用Prophet时需要对自定义参数有一些了解。
2. 安装
通过Anaconda安装Prophet非常简单(用pip安装可能会踩坑):
# 1. 创建虚拟环境
conda create -n prophet python=3.7
# 2. 激活虚拟环境
source activate prophet
# 3. 通过conda-forge安装prophet
conda install -c conda-forge fbprophet
3. 基本用法
Prophet的基本用法分以下几步:
- 读取训练数据
- 初始化prophet模型
- 训练prophet模型
- 生成测试集
- 进行预测
# 导入包
import pandas as pd
from fbprophet import Prophet
# 读数据
# df(dataframe)需要包含两列,一列 date,一列 y
df = pd.DataFrame({
'ds': pd.date_range('20071210',periods=3700),
'y': [np.random.rand() + np.cos(0.05 * x) for x in range(3700)]
})
# 初始化 prophet 模型
m = Prophet()
# 训练 prophet 模型
m.fit(df)
# 生成预测数据(默认天粒度)
future = m.make_future_dataframe(periods=365)
# 使用训练好的模型进行预测
forecast = m.predict(future)
# 预测绘图
fig1 = m.plot(forecast)
# 分量绘图
fig2 = m.plot_components(forecast)
数据示例
输入和输出数据格式如下:
输入数据 df: pd.DataFrame
| - | ds | y |
|---|---|---|
| 0 | 2007-12-10 | 9.590761 |
| 1 | 2007-12-11 | 8.519590 |
| 2 | 2007-12-12 | 8.183677 |
| 3 | 2007-12-13 | 8.072467 |
| 4 | 2007-12-14 | 7.893572 |
预测结果 forecast: pd.DataFrame
| ds | yhat | yhat_lower | yhat_upper | |
|---|---|---|---|---|
| 3265 | 2017-01-15 | 8.212942 | 7.463560 | 8.937215 |
| 3266 | 2017-01-16 | 8.537993 | 7.790259 | 9.267492 |
| 3267 | 2017-01-17 | 8.325428 | 7.525675 | 9.059391 |
| 3268 | 2017-01-18 | 8.158059 | 7.433634 | 8.883627 |
| 3269 | 2017-01-19 | 8.170046 | 7.431801 | 8.840703 |
更多的参数配置请参考官方示例[3]。
4. 算法原理
Prophet基于时间序列的分解,把时间序列分解成四个部分,分别是趋势项,季节项,节日项和剩余项,将这几项之和作为预测值:
$$ y(t)=g(t)+s(t)+h(t)+\epsilon_{t} $$
其中$g(t)$表示趋势项,它表示时间序列非周期性的变化趋势;$s(t)$ 表示周期项,或者称为季节项,一般来说是以日或周或者年为单位;$h(t)$ 表示节假日项,表示在当天是否存在节假日;$\epsilon_{t}$ 表示误差项或者称为剩余项。
Prophet 算法就是通过拟合这几项,然后最后把它们累加起来就得到了时间序列的预测值。
4.1 趋势模型
在 Prophet 中,趋势项可以有两种选择,一个是饱和增长模型(saturating model),也称逻辑回归模型(logistic function);另一个是分段线性模型(piecewise linear model)。下面分别介绍这两个模型:
饱和增长模型
在自然界中,很多趋势是非线性增长的,比如人口,经济增速等。它们通常都有一定的承载上界,比如facebook的用户数量,这种增长常用 Logistic 增长模型进行建模。
Logistic 函数的基本形式是:
$$ y=\frac{1}{1+\exp ^{-x}} $$
函数图像如下图所示:
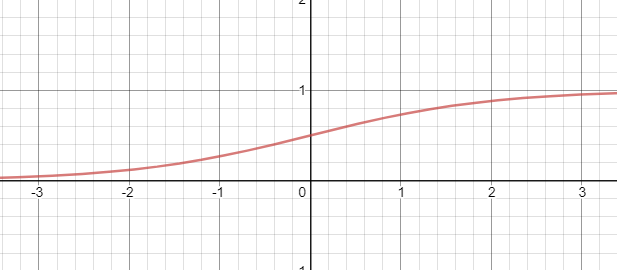
在实际情况中,拟合趋势$g(t)$需要在 Logistic 模型上增加一些参数:
$$ g(t)=\frac{C}{1+\exp ^ {-k(t-m)}} $$
其中$C$称为曲线的最大渐近值(也称承载上界),$k$ 表示曲线的增长率,$m$ 表示曲线的中点。下图为$k$发生变动时的函数变化。
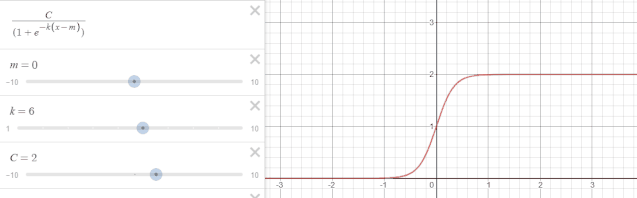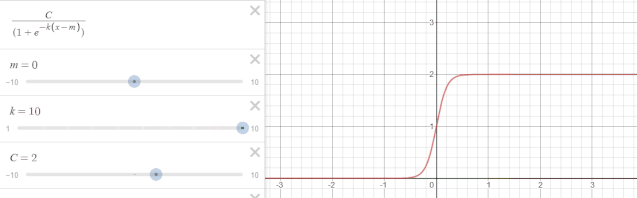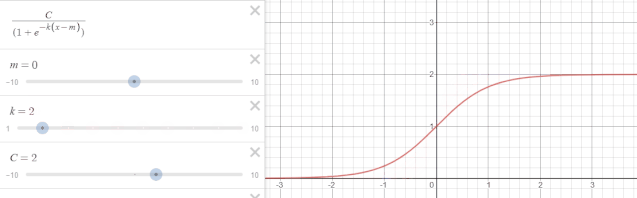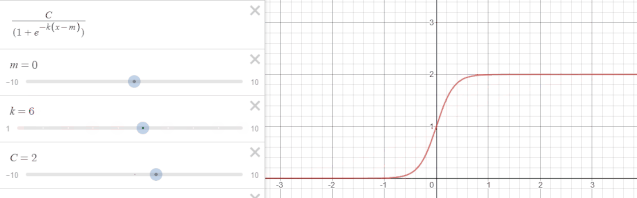
当 $C=1,k=1,m=0$ 时,恰好就是 sigmoid 函数的形式。
渐进值$C$可能会随时间发生变化,所以将$C$替换为随时间变化的函数 $C(t)$。
$$ g(t)=\frac{C(t)}{1+\exp ^ {-k(t-m)}} $$
增长率$k$也可能会随时间变化,例如特定的事件会改变增长率。为了适应增长率的变化,Prophet引入变点(changepoint)的概念,变点前后时序的趋势发生了变化。
Prophet默认会设置25个变点(n_changepoints=25),设置范围是前80%的时序数据(changepoint_range=0.8),也就是在时间序列的前 80% 的区间内会设置变点,而且是均匀分布,如下图所示。
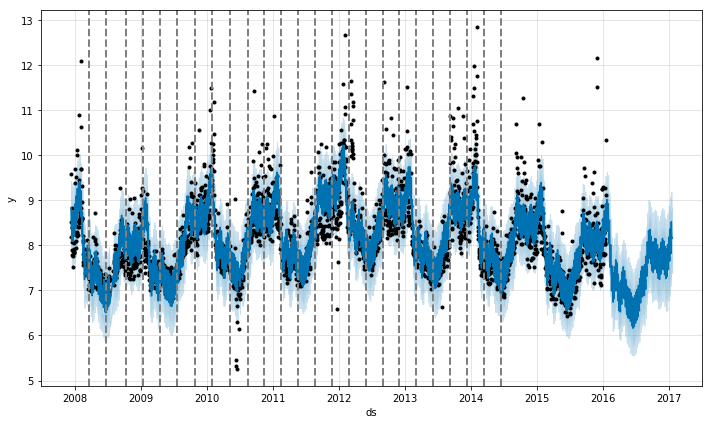
假设在时间序列中设置$S$个变点,每个变点的时间戳为$s_j,j=1,…,S$。定义在变点处增长率$k$的变化率为$\boldsymbol{\delta} \in \mathbb{R}^{S}$(可以理解为曲线的二阶导数,增长率的一阶导数),$\delta_j$表示变点在时间$s_j$上增长率的变化,若定义基准变化率为$k$,那么时间$t$上的增长率$k_t$可以定义为:
$$ k_t = k+\sum_{j : t>s_{j}} \delta_{j} $$
$k_t$为时间$t$之前变点的增长变化率累加和,再加上基准变化率$k$。使用向量的形式重写上述公式,简化为:
$$ k_t = k+\mathbf{a}(t)^{\top} \boldsymbol{\delta} $$
其中,
$$ a(t)=\begin{cases} 1, & \text { if } t \geq s_{j} \newline 0, & \text { otherwise } \end{cases} $$
增长率$k$变化的时候,偏移量$m$也必须跟着变化,否则函数会不连续。
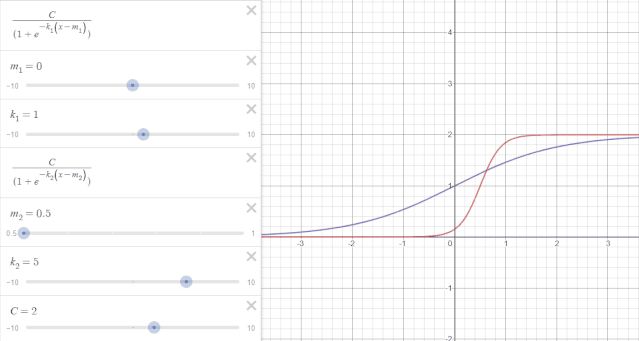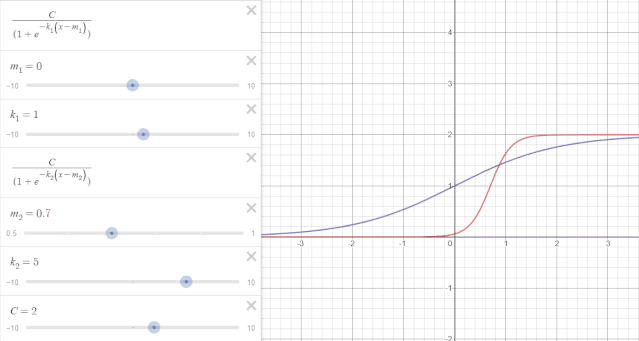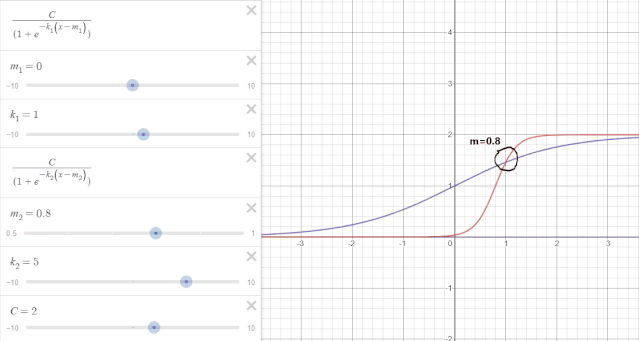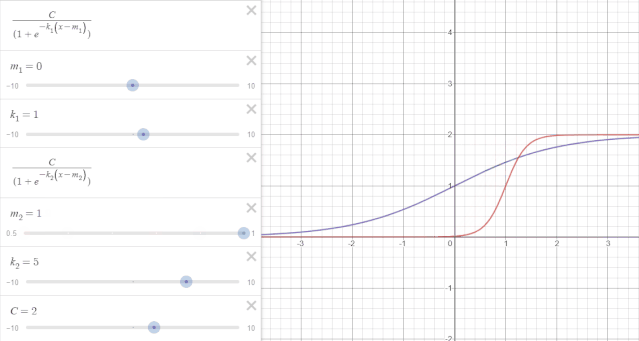
举一个例子来说:如图所示,纵轴表示时序趋势值,横轴表示时间$t$。假设一开始的趋势变化如紫线所示,增长率$k_1=1$,偏移量$m_1=0$,$t=1$时出现变点,增长率变换为$k_2=5$,如红线所示,但是在变点处,也就是$t=1$处红紫线不相交,造成趋势不连续。可通过修正偏移量$m$使变点前后趋势连续。
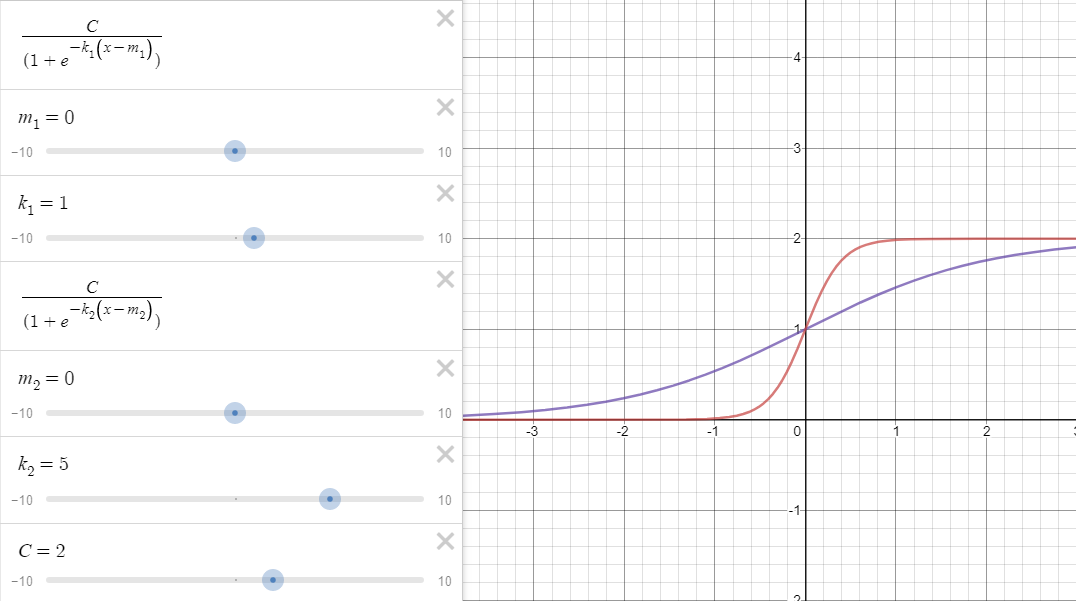
如下图所示,当偏移量$m$修正为0.8时,变点前后趋势项连续。
在变点$j$偏移量的更新可以表示为:
$$ \gamma_{j}=\left(s_{j}-m-\sum_{l\leq j-1} \gamma_{l} \right) \left(1-\frac{k+\sum_{l\leq j-1} \delta_{l}}{k+\sum_{l \leq j} \delta_{l}} \right) $$
最后logistic model表示为:
$$ g(t)=\frac{C(t)}{1+\exp \left(-\left(k+\mathbf{a}(t)^{\top} \boldsymbol{\delta}\right)\left(t-\left(m+\mathbf{a}(t)^{\top} \boldsymbol{\gamma}\right)\right)\right)} $$ 注意:在选择逻辑回归模型作为趋势项时,需要人为指定$C(t)$。
分段线性模型
对于那些不显式为饱和增长的预测问题,Prophet还提供了另外一种简洁且有用的趋势模型——分段线性模型。变点之间的趋势是线性函数,如下图所示。
线性函数指的是 $y=kx+b$, 而分段线性函数指的是在每一个子区间上,函数都是线性函数,但是在整段区间上,函数并不完全是线性的。
和逻辑回归模型相同,分段线性模型同样加入了变点,分段线性模型可表示为:
$$ g(t)=\left(k+\mathbf{a}(t)^{\top} \boldsymbol{\delta}\right) t+\left(m+\mathbf{a}(t)^{\top} \boldsymbol{\gamma}\right) $$
其中,$k$ 表示初始增长率,$k+\mathbf{a}(t)^{\top} \boldsymbol{\delta}$表示时间$t$的增长率,$m+\mathbf{a}(t)^{\top} \boldsymbol{\gamma}$为修正后的偏移量,其中$\gamma_j=-s_j\delta_j$,$\gamma_j$的设定和逻辑回归模型有所区别。
4.2 季节模型
通常时间序列包含多周期季节性(multi-period seasonality),比如寒暑假的影响以年为周期,工作日的影响以周为周期等。
Prophet采用傅里叶级数来拟合周期效应。傅里叶级数能将任何周期函数或周期信号分解成一个(可能由无穷个元素组成的)简单振荡函数的集合,即正弦函数和余弦函数。
举一个例子,以$2\pi$为周期的时间序列可以用下式傅里叶级数表示:
$$ f(x) = \sum_{n=0}^N\left(\frac{a_n\sin\left(\left(2n+1\right) x\right)}{\left(2n+1\right)\pi}\right) $$
可视化效果如下:
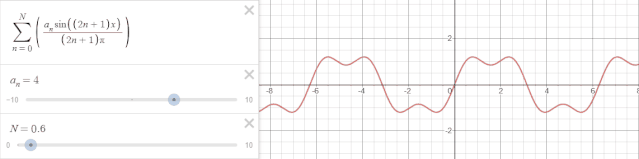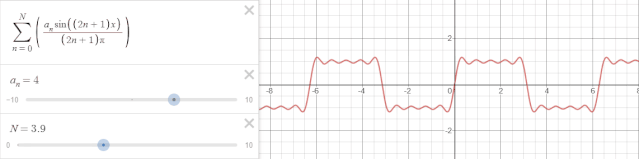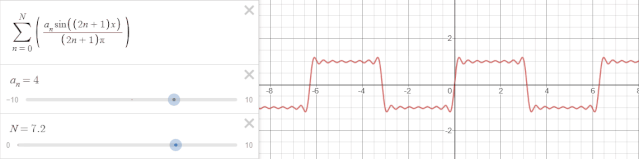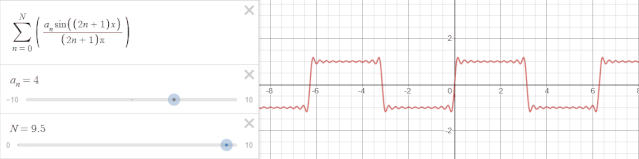
$N$越大,也就是级数越多,越趋向于对周期的过拟合,在Prophet中,可以通过参数调整傅里叶级数。
假设一个以$P$为周期的时间序列,它的傅里叶级数形式为:
$$ s(t)=\sum_{n=1}^{N}\left(a_{n} \cos \left(\frac{2 \pi n t}{P}\right)+b_{n} \sin \left(\frac{2 \pi n t}{P}\right)\right) $$
Prophet内置了三种周期:年、周和日。当$P=365.25$时,表示以年为周期,当$P=7$时,表示以周为周期,当$P=1$时,表示以天为周期。
Prophet 作者按照经验,设置了这些周期的默认级数,对于以年为周期的序列,$N=10$ ;对于以周为周期的序列,$N=3$ ,对于以天为周期的序列,$N=4$ 。
使用傅里叶级数拟合周期性需要估计$2N$个参数,用向量$\boldsymbol{\beta}$表示:
$$ \boldsymbol{\beta} = \left[a_{1}, b_{1}, \ldots, a_{N}, b_{N}\right]^{\top} $$
对于年周期($N=10$)来说,它的季节性傅里叶特征可以表示为:
$$ X(t)=\left[\cos \left(\frac{2 \pi(1) t}{365.25}\right),\sin \left(\frac{2 \pi(1) t}{365.25}\right), \ldots, \cos \left(\frac{2 \pi(10) t}{365.25}\right),\sin \left(\frac{2 \pi(10) t}{365.25}\right)\right] $$
时间$t$的季节性分量就可以表示为:
$$ s(t) = X(t)\boldsymbol{\beta} $$
4.3 节假日模型
节假日和事件往往对时间序列预测有较大的影响,且通常不遵循周期模式,所以无法用季节性模型去建模节日。另外,节日和时间也有可能是非稳定周期的,比如中国的农历节日,NBA的决赛时间,手机的新品发布时间等等。
不同的节假日可以看成相互独立的模型,且不同的节假日有不同的前后窗口值,表示该节假日会影响前后一段时间的时间序列。比如春节有15天的窗口,而清明节只有3天窗口期。
对于第$i$个节假日来说,$D_i$表示该节假日过去和未来时间的集合,比如下表列举的是感恩节的集合。
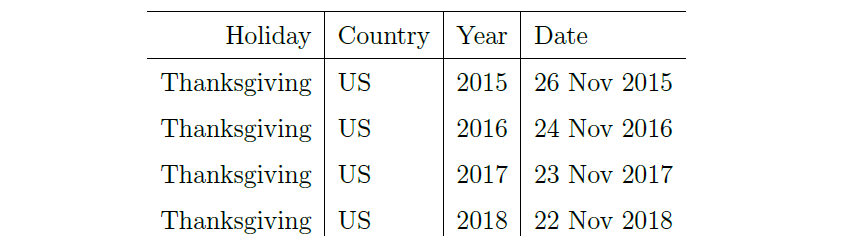
用参数$\kappa_{i}$表示节日$i$的分量,向量$\boldsymbol{\kappa} = (\kappa_1,…,\kappa_L)$表示$L$个节假日的分量。
用指示函数$Z(t)$表示在时间$t$所处的节日,类似于one-hot形式:
$$ Z(t)=\left[1\left(t \in D_{1}\right), \ldots, 1\left(t \in D_{L}\right)\right] $$
时间$t$的节日分量可以表示为
$$ h(t)=Z(t) \boldsymbol{\kappa} $$
其中$\boldsymbol{\kappa} \sim \operatorname{Normal}\left(0, \nu^{2}\right)$,服从正态分布,其中$v$是可调参数,默认值是10。当值越大时,表示节假日对模型的影响越大;当值越小时,表示节假日对模型的效果越小。
4.4 Prophet模型
综上,Prophet的预测模型[4]可以表示为:
$$ {\hat y}(t)=g(t)+s(t)+h(t)+\epsilon_{t} $$
若选择逻辑回归模型作为趋势模型,上式可演变为:
$$ {\hat y}(t)=\frac{C(t)}{1+\exp \left(-\left(k+\mathbf{a}(t)^{\top} \boldsymbol{\delta}\right)\left(t-\left(m+\mathbf{a}(t)^{\top} \boldsymbol{\gamma}\right)\right)\right)}+X(t)\boldsymbol{\beta}+Z(t) \boldsymbol{\kappa}+\epsilon_{t} $$
若趋势项为分段线性模型:
$$ {\hat y}(t)=\left(k+\mathbf{a}(t)^{\top} \boldsymbol{\delta}\right) t+\left(m+\mathbf{a}(t)^{\top} \boldsymbol{\gamma}\right)+X(t)\boldsymbol{\beta}+Z(t) \boldsymbol{\kappa}+\epsilon_{t} $$
训练时,采用L-BFGS做最大似然估计(maximum likelihood estimate)训练出模型中的参数。
5. 源码
若想完全掌握Prophet模型,还是需要去撸一遍源码,一方面是在使用时心里有个底,另一方面是为了更好的调参。
通过 debug 以下代码走一遍 Prophet 的流程。
# 初始化 prophet 模型
m = Prophet()
# 训练 prophet 模型
m.fit(df)
# 生成预测数据(默认天粒度)
future = m.make_future_dataframe(periods=365)
# 使用训练好的模型进行预测
forecast = m.predict(future)
5.1 模型初始化
首先,初始化prophet模型:
m = Prophet()
初始化的时候可以指定一些参数,若不指定,Prophet会指定参数的默认值。具体的参数默认初始化如下:
# func __init__()
# 初始化参数(可设置)
growth='linear', # 趋势选择 'linear'或'logistic'(分段线性 或 逻辑回归)
changepoints=None, # 变点时间(Series)
n_changepoints=25, # changepoint个数:默认25
changepoint_range=0.8, # changepoint范围:默认前80%
yearly_seasonality='auto', # 年周期性,可设 True or False
weekly_seasonality='auto', # 周周期性,可设 True or False
daily_seasonality='auto', # 日周期性,可设 True or False
holidays=None, # 节假日,默认为None
seasonality_mode='additive', # 周期叠加方式,'additive'或'multiplicative'
seasonality_prior_scale=10.0, # 周期先验值
holidays_prior_scale=10.0, # 节假日先验值
changepoint_prior_scale=0.05, # 变点先验值
mcmc_samples=0, #
interval_width=0.80, #
uncertainty_samples=1000, #
# 其他参数
start = None # 训练集开始时间
y_scale = None # 训练集 y 最大值
logistic_floor = False
t_scale = None # 训练集时间跨度
changepoints_t = None # 变点在时间轴的比例
seasonalities = OrderedDict({})
extra_regressors = OrderedDict({})
country_holidays = None # 指定国家节日,中国为'CN'
stan_fit = None # pystan拟合时的参数
params = {} # 训练得到的参数
history = None # 输入数据
history_dates = None # 历史数据中的时间
train_component_cols = None # 每列特征对应的类别
component_modes = None # {'additive':[],'multiplicative':[]}
train_holiday_names = None # 配置的 holiday 名称
其他参数都比较好理解,重点说一下后缀带有prior_scale的参数。它们是控制变量的拟合程度的参数,可以理解为正则项系数,值越高,越趋向过拟合,值越低越趋向平滑。
初始化时,Prophet 会验证以下参数:
func validate_inputs() # 验证输入
1. growth not in ('linear', 'logistic') # 验证'growth'
2. (changepoint_range < 0) or (changepoint_range > 1) # 验证changepoint_range区间
3. holidays lower_window/upper_window # 验证holiday名称和窗口值
4. seasonality_mode not in ['additive', 'multiplicative'] # 验证'seasonality_mode'
以上,初始化的部分就结束了。
5.2 模型训练
接下来便可以喂入数据训练模型了:
m.fit(train_data)
其中,train_data是 pd.DataFrame 类型,必须包含两列:
| ds | y |
|---|---|
| 日期 | 值 |
如果growth设为'logistic',必须还有一列cap:
| ds | y | cap |
|---|---|---|
| 日期 | 值 | 承载上界 |
这里的cap其实就是趋势模型中的$C(t)$,需要人为输入。
喂入数据后,开始训练Prophet模型,fit() 函数中的主要步骤如下:
- 扩充dataframe
- 设置季节性参数
- 生成季节性特征
- 设置变点
- 初始化变点参数
- 初始化stan模型(prophet采用 pystan[5] 作为线性回归模型)
- 训练stan模型
简单来说,这些步骤可以合并成最基本的机器学习范式:1-5步生成特征矩阵(如下图所示),6-7步训练线性回归模型(采用pystan)。
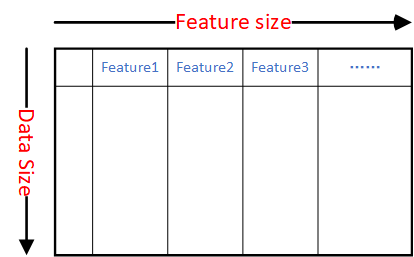
1. 扩充dataframe
首先通过 setup_dataframe() 函数为 train_data 增加三列,分别对时间和训练数据进行归一化。
df['floor']=0 # 最小值(默认)
df['t'] = (df['ds'] - self.start) / self.t_scale # 时间归一化
df['y_scaled'] = (df['y'] - df['floor']) / self.y_scale # y 值归一化
其中
t_scale = df['ds'].max() - df['ds'].min() # 最大时间和最小时间的差值
y_scale = (df['y'] - floor).abs() # y最大值的绝对值
train_data:
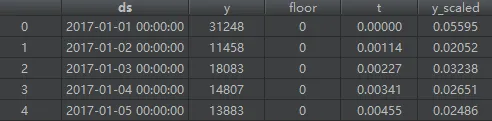
2. 设置季节性参数
若初始化模型时没有设置季节性参数,Prophet 会通过 set_auto_seasonalities() 自动检测训练数据并设置季节性参数,主要有以下几个参数:
min_dt: 检测最小时间间隔yearly_disable:若训练数据时间小于两年,禁用年周期weekly_disable:若训练数据时间小于两周或min_dt>=一周,禁用周周期daily_disable:若训练数据时间小于两天或min_dt>=一天,禁用天周期fourier_order:parse_seasonality_args(): 获取内置季节性的傅里叶级数(见下图)- 若季节性没有
disable,设置默认季节性参数:
# prophet 内置的 [年/月/日] 周期季节性参数:
# period:周期
# fourier_order:傅里叶级数
# prior_scale:先验值,用于调整拟合度
# mode:加法或乘法模型
self.seasonalities['yearly'] = {
'period': 365.25,
'fourier_order': fourier_order, # 默认为 10
'prior_scale': self.seasonality_prior_scale, # 10
'mode': self.seasonality_mode, # additive
'condition_name': None
}
self.seasonalities['weekly'] = {
'period': 7,
'fourier_order': fourier_order, # 默认为 3
'prior_scale': self.seasonality_prior_scale, # 10
'mode': self.seasonality_mode, # additive
'condition_name': None
}
self.seasonalities['daily'] = {
'period': 1,
'fourier_order': fourier_order, # 默认为 4
'prior_scale': self.seasonality_prior_scale, # 10
'mode': self.seasonality_mode, # additive
'condition_name': None
}
3. 生成季节性特征
设定季节性参数后,通过 make_all_seasonality_features() 函数生成包含季节性特征的dataframe,包括季节特征、节日特征和自定义特征。make_all_seasonality_features的代码结构如下所示:
make_seasonality_features(): 生成季节性特征fourier_series():生成傅里叶级数特征
make_holiday_features():生成节日特征construct_holiday_dataframe(): 构建节假日dataframemake_holidays_df(): 根据国家和年份构建节假日dataframe
make_holiday_features():构建节假日特征
additional regressors():生成自定义特征regressor_column_matrix()add_group_component
- 返回:
seasonal_features,prior_scales,component_cols,modes
首先,通过 make_seasonality_features 构建季节性特征,这里主要采用傅里叶级数构建特征(原理见第4节)。代码如下:
# fourier_series: 生成傅里叶级数特征
np.column_stack([
fun((2.0 * (i + 1) * np.pi * t / period)) # t 为 1970-01-01 到现在的天数 array
for i in range(series_order)
for fun in (np.sin, np.cos)
])
下面两张图展示了年和周两种周期的傅里叶级数特征:
year_seasonality: $data_size \times 20$维的dataframe,每一行是该时间的20维的 year_fourier 特征

week_seasonality: $data_size \times 6$维的dataframe,每一行是该时间的6维的 week_fourier 特征

其次, make_holiday_features 函数根据节日配置参数构建节假日dataframe:holiday_df,如下表所示:

并根据节假日表生成对应的节假日特征。
holiday_feature: $data_size \times len(holiday)$维的特征,类似于one-hot表示

另外,Prophet还支持加入自定义特征,源码中 additional_regressors 函数绑定自定义特征。
最后,合并seasonality、holiday、addtional特征,生成总的季节性特征seasonal_feature:

regressor_column_matrix 函数对 seasonal_feature 进行加工,生成每一维特征对应的 one-hot 向量,方便之后的模型解释和可视化:
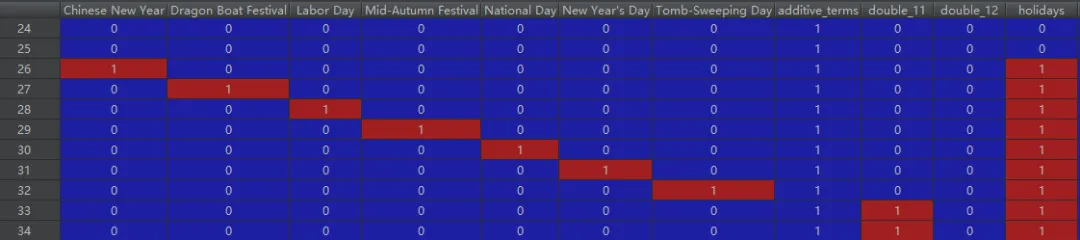
modes:函数make_all_seasonality_features的返回结果,它是一个记录加法变量和乘法变量的字典 (dict) 。
<class 'dict'>:
{'additive': [
'yearly',
'weekly',
'spring_festival',
'double_11',
'double_12',
'yx_411',
'yx_618',
"New Year's Day",
'Chinese New Year',
'Tomb-Sweeping Day',
'Labor Day',
'Dragon Boat Festival',
'Mid-Autumn Festival',
'National Day',
'additive_terms',
'extra_regressors_additive',
'holidays'],
'multiplicative': [
'multiplicative_terms',
'extra_regressors_multiplicative']
}
4. 设置变点
set_changepoint: 变点的设置有以下几种情况。
- 参数显式传递变点
- 自动生成变点
- 不使用变点
如果自动设置变点,Prophet会默认在前80%的数据中选择25个变点。
changepoints 示例如下: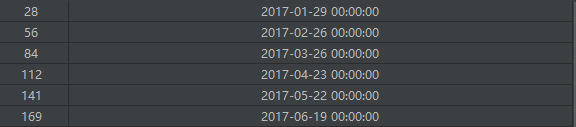
5. 初始化变点参数
linear_growth_init:分段线性增长模型,初始化斜率$k$和截距$m$logistic_growth_init:逻辑斯蒂增长模型,初始化增长率$k$和偏移量$m$
下图为实际计算过程中$k$和$m$的初始化值。
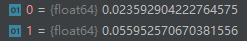
6. 初始化stan模型
Prophet预置了一份模型,初始化时会加载进来:
model = prophet_stan_model
以下是 stan 模型所用到的参数:
dat = {
'T': history.shape[0],
'K': seasonal_features.shape[1],
'S': len(self.changepoints_t),
'y': history['y_scaled'],
't': history['t'],
't_change': self.changepoints_t,
'X': seasonal_features,
'sigmas': prior_scales,
'tau': self.changepoint_prior_scale,
'trend_indicator': int(self.growth == 'logistic'),
's_a': component_cols['additive_terms'],
's_m': component_cols['multiplicative_terms'],
}
7. 训练stan模型
这里简单介绍一下 Stan。Stan其实是一种用于统计推断的概率编程语言。以线性回归为例,下面是最简单的线性回归模型,具有单个预测变量,斜率和截距系数以及正态分布的噪声。该模型可以编写为:
$$ y_{n}=\alpha+\beta x_{n}+\epsilon_{n} \quad \text { where } \epsilon_{n} \sim \operatorname{normal}(0, \sigma) $$
上式等效于对于残差的采样:
$$ y_{n}-\left(\alpha+\beta X_{n}\right) \sim \operatorname{normal}(0, \sigma) $$
并进一步简化为:
$$ y_{n} \sim \operatorname{normal}\left(\alpha+\beta X_{n}, \sigma\right) $$
Prophet的 stan 模型可直接写为:
# stan分段线性模型
# y ~ 趋势项 * (1 + 乘法项)+ 加法项(季节、节假日) + 残差
y ~ normal(
linear_trend(k, m, delta, t, A, t_change)
.* (1 + X * (beta .* s_m))
+ X * (beta .* s_a),
sigma_obs
)
vector linear_trend(
real k, # 斜率
real m, # 截距
vector delta, # 增长率变化率向量
vector t, # 时间
matrix A, # 标志位
vector t_change
) {
return (k + A * delta) .* t + (m + A * (-t_change .* delta));
}
5.3 生成测试集
通过 make_future_dataframe 函数在训练集基础上往后延 periods 的时间作为测试集。
future = m.make_future_dataframe(periods=90)
5.4 预测
forecast = m.predict(future)
第一步,通过setup_dataframe()函数初始化测试集dataframe。
第二步,对测试集进行趋势预测,这里展示分段线法(piecewise_linear)的预测过程
再回顾一下分段线性模型的公式: $$ g(t)=\left(k+\mathbf{a}(t)^{\top} \boldsymbol{\delta}\right) t+\left(m+\mathbf{a}(t)^{\top} \boldsymbol{\gamma}\right) $$
源码中的趋势计算如下:
# 梯度和截距累加
# Intercept changes
gammas = -changepoint_ts * deltas
# Get cumulative slope and intercept at each t
k_t = k * np.ones_like(t) # k 为初始斜率
m_t = m * np.ones_like(t) # m 为初始截距
for s, t_s in enumerate(changepoint_ts):
indx = t >= t_s # 大于t_s的部分进行累加
k_t[indx] += deltas[s] # 累加斜率
m_t[indx] += gammas[s] # 累加截距
trend = k_t * t + m_t
trend = trend * self.y_scale + df['floor'] # scale还原
通过累加计算每一个变点之间的$k$和$m$,最后乘以缩放因子 y_scale,预测出趋势。
第三步,周期性预测:通过 predict_seasonal_components 函数预测 seasonality, holidays 和 added regressors。
与训练过程类似,通过 make_all_seasonality_features 函数构建预测日期的季节性特征,生成类似于训练集的特征矩阵。

计算lower_p, upper_p,也就是预测结果的上下界。
for component in component_cols.columns:
beta_c = self.params['beta'] * component_cols[component].values
comp = np.matmul(X, beta_c.transpose())
if component in self.component_modes['additive']:
comp *= self.y_scale
data[component] = np.nanmean(comp, axis=1)
data[component + '_lower'] = np.nanpercentile(
comp, lower_p, axis=1,
)
data[component + '_upper'] = np.nanpercentile(
comp, upper_p, axis=1,
)
计算每个周期性特征分量 seasonal_components

第四步,计算趋势和yhat的上下界(uncertainty)。
sample_posterior_predictive:
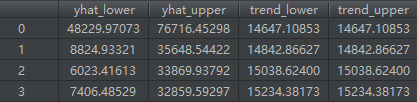
第五步,计算y_hat。
df2 = pd.concat((df[cols], intervals, seasonal_components), axis=1)
df2['yhat'] = (
df2['trend'] * (1 + df2['multiplicative_terms'])
+ df2['additive_terms']
)
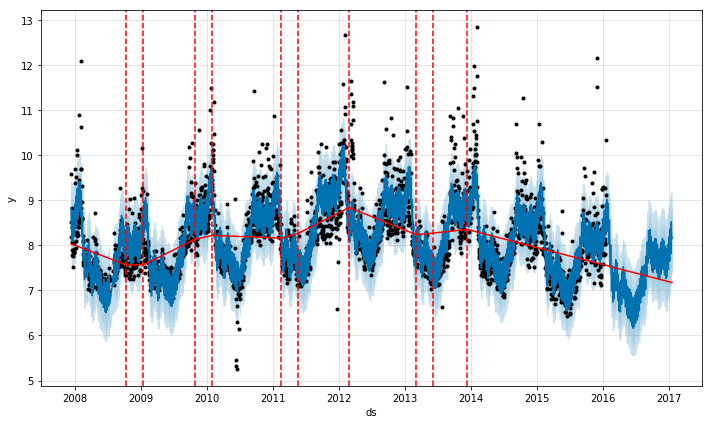
下图为预测结果的可视化示例,分别展示了trend、holidays、weekly、yearly分量,提供了一定的可解释性。
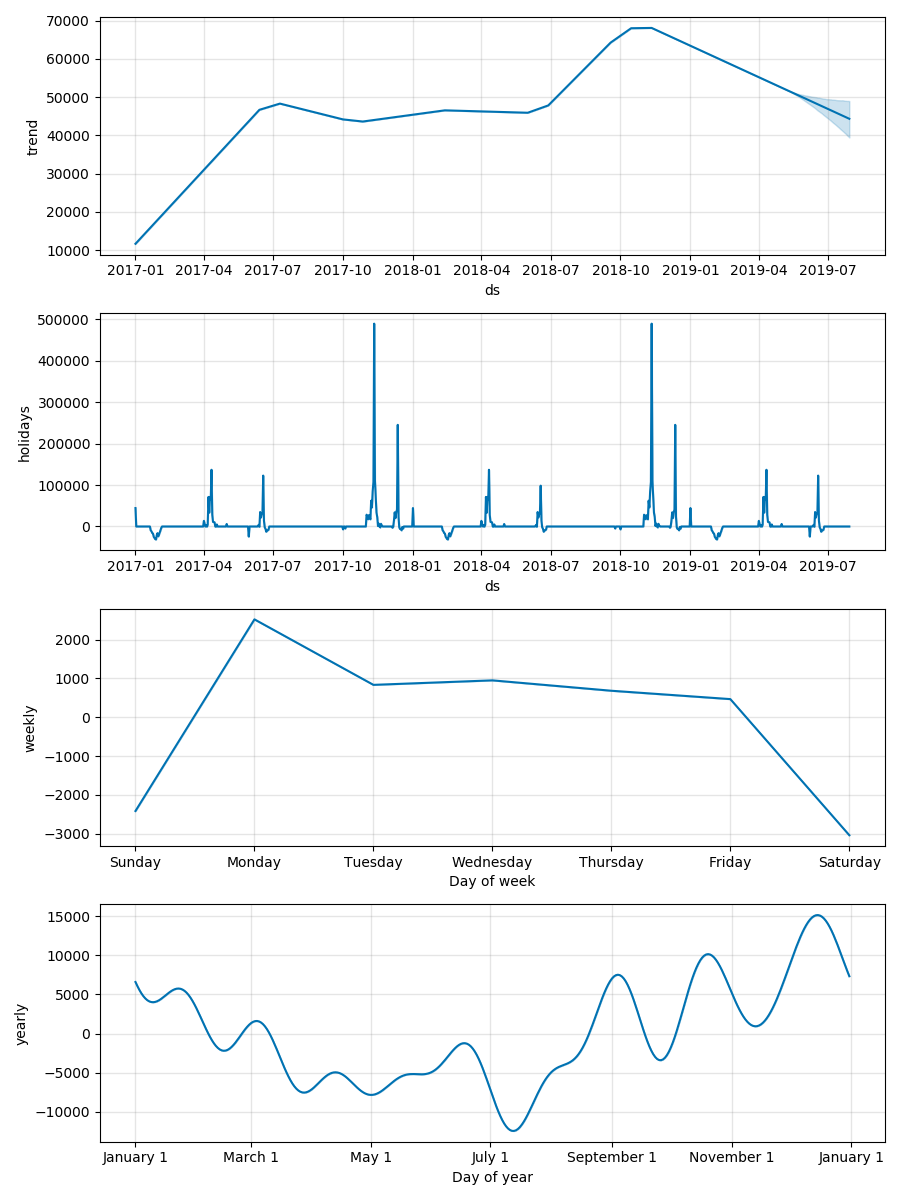
6. 总结
Prophet 针对一维时间序列进行建模,将时间序列分为趋势、季节、节日三部分特征,并输出预测结果的上下界,同时保证了预测结果的可解释性。从原理上来说,Prophet是一个自动特征提取的线性回归模型,适用于少特征、规律性高、单维度的时间序列场景。若业务场景有多维度特征,多时间序列,复杂度高,则不适用Prophet。
7. 参考
[1]: Prophet官网:https://facebook.github.io/prophet/docs/quick_start.html#python-api
[2]: Prophet代码地址: https://github.com/facebook/prophet
[3]: Prophet示例:https://github.com/facebook/prophet/tree/master/notebooks
[4]: Prophet预测模型论文:https://peerj.com/preprints/3190/
[5]: stan模型:https://pystan.readthedocs.io/en/latest/
[6]: Facebook 时间序列预测算法 Prophet 的研究. https://zhuanlan.zhihu.com/p/52330017