销量预测中的误差指标分析
目录
本文介绍一些销量预测相关的误差指标。它们可以被分为两类:绝对误差和绝对百分比误差。前两节介绍销量预测问题及相关概念。第 3 节我们介绍 3 种绝对误差,并比较它们对异常值的敏感性。
由于绝对误差不适合比较多个商品或多个时段的预测结果,在第 4 节我们介绍 3 种百分比误差。在这一节,我们重点强调了它们的优点和缺陷。第 5 节是误差指标比较结果的汇总。
在第 6 节中,我们用一个例子充分说明了百分比误差容易引发的问题,并提醒读者在实际中必须确认预测目标与误差的一致性。在第 7 节,我们给出一些结论和实际使用中的建议。
1. 销量预测
销量预测问题是供应链管理中的一个基本问题。销量预测可用来指导商品采购,新品立项,销售计划,库存平衡和资源调度等业务。因此,预测"效果"的好坏将直接影响这些业务的质量 (注: 不同业务可能要求不同的预测"效果")。我们一般用预测销量和真实销量之间的误差来评估销量预测结果或模型的好坏。直观地讲,预测销量与真实销量越"接近"则误差越小,反之则误差越大。
为方便描述,我们考虑如下简化的销量预测问题。
销量预测 预测一个商品未来 1 到 n 天的销量。用 $x_t$ 和 $y_t$ 分别代表商品第 $t$ 天的实际销量和预测销量,其中 $t=1, 2, …, n$。因此我们需要估计实际销量 $\set{x_1, x_2, … x_n}$ 与预测销量 $\set{y_1, y_2, … y_n}$ 之间的误差。
2. 基本概念
首先考虑第 $t$ 天的实际销量 $x_t$ 和预测销量 $y_t$。 定义两种误差:
绝对误差 (Absolute Error): $e_t = |x_t-y_t|$。
绝对百分比误差 (Absolute Percentage Error): $p_t = 100 e_t / x_t$。
我们通过一个简单的例子来比较两种误差。
例. 假设 $x_1=1000, y_1= 1020, x_2=1, y_2=11$。
- 绝对误差: $e_1=20, e_2=10$。优点是能直接反映误差的大小;缺点是依赖标度 (Scale-dependent), 即, 它依赖观测值的标度(单位),因此不适合比较不同商品或不同时段之间的误差。
- 绝对百分比误差: $p_1=2, p_2= 1000$。优点是不依赖标度(Scale-free);缺点是要求$x_t\neq 0$,而这个条件在实际中往往不满足。此外,即使满足条件 $x_t\neq 0$,当 $x_t$ 比较小时,容易造成 $p_t = 100e_t /x_t$ 非常大(从而严重影响总体误差)。
3. 绝对误差
下面考虑实际销量 ${x_1, x_2, … x_n}$ 与预测销量 ${y_1, y_2, … y_n}$ 之间的误差指标。我们先介绍三种绝对误差指标。
平均绝对误差 (Mean Absolute Error - MAE)
$$\text{MAE} = \frac{1}{n}\sum_{t=1}^n e_t$$
几何平均绝对误差 (Geometric Mean Absolute Error - GMAE)
$$\text{GMAE} = \left(\Pi_{t=1}^n e_t\right)^{\frac{1}{n}}$$
- 根均方误差 (Root Mean Square Error - RMSE)
$$\text{RMSE} = \sqrt{\frac{1}{n}\sum_{t=1}^n e_t^2}$$
误差比较
- 可以证明:$\text{RMSE} \geq \text{MAE} \geq \text{GMAE}$。这个关系也体现了它们对异常值的敏感程度(从左到右, 从高到低)。
- GMAE 对异常值不太敏感,其误差值比较稳定,因而适合用来比较预测模型的优劣。但它要求 $e_t\neq 0$(否则GMAE=0)。此外,由于需要开 n 次根,其计算相对 MAE 耗时较大。
- RMSE 和 MAE 对异常值比较敏感。换句话说,单个时段的绝对误差 $e_t$ 可能会较大地影响整体误差,从而导致误差值会随着预测值的变化呈现较大的波动。因此,在使用中我们需要先剔除异常值。
- 由于绝对误差依赖标度,它们不适合用来比较不同商品或不同时期预测结果的误差水平。
4. 绝对百分比误差
为了克服绝对误差依赖标度的缺点,一个自然的想法是考虑百分比误差。在实际使用中,人们常常盲目地使用直观易懂的误差指标(例如下文提到的MAPE),并忽略了百分比误差自身的一些缺陷,从而导致误差的降低并不能带来期望中预测效果的提升。本节我们重点强调绝对百分比误差的缺陷以及使用时需要注意的事项。
4.1 MAPE
MAPE 是 Mean Absolute Percentage Error 的缩写,即 平均绝对百分比误差。
$$\text{MAPE} = \frac{1}{n}\sum_{t=1}^n p_t $$
优点
直观, 容易计算
缺点
- 它要求 $x_t\neq 0$,否则 $p_t=+\infty$,从而导致 $\text{MAPE}=+\infty$。
- MAPE没有上界,因此对异常值敏感。当某个 $p_t$ 非常大时,会导致 MAPE 的值也显著变大。
- 如果使用MAPE作为误差评价指标,** $p_t$ 的不对称性会导致预测销量低于实际销量**(解释如下)。
$p_t$的不对称性
给定实际销量 $x_t$, 当预测销量 $y_t$ 从 0 变化到 $+\infty$ 时,分别考虑"低估"和"高估"时 $p_t$ 的上界。
- 低估: $y_t < x_t$, 此时 $p_t\leq 100$,即 $p_t$ 上界为 100;
- 高估: $y_t > x_t$, 此时 $p_t\leq +\infty$, 即 $p_t$ 上界为无穷大。
由于高估会带来较大惩罚, 为了最小化 MAPE 值, 算法会倾向低估, 从而导致预测的销量偏低。
4.2 SMAPE
SMAPE 是 Symmetric Mean Absolute Percentage Error 的缩写, 即对称的平均绝对百分比误差。
为了弥补 $p_t$ 的不对称性, M3-竞赛1 和 IJCAI-172 数据挖掘竞赛采用了所谓"对称的"MAPE作为误差评价指标。定义如下:
$$\text{SMAPE} = \frac{1}{n} \sum_{t=1}^{n} p’_t, \quad \text{其中 } p’_t = \frac{200e_t}{x_t + y_t}.$$
优点
- 始终可计算(当 $x_t+y_t=0$ 时, 定义 $p_t=0$)。
- SMAPE有界, 即: $0 \leq \text{SMAPE} \leq 200$。
- 形式上满足对称性, 即低估和高估时 $p’_t的$ 上界都是200。
缺点
- $p’_t$ 的意义不直观, 缺乏解释性。
- 在实际的销量预测中,由于销量的上界通常是有限的(通过经验可以预估),因而即使出现"高估"的情形,预测销量 $y_t$ 一般不会超过实际销量的常数倍(例如不超过10倍)。从这个角度来看,高估时误差 $p’_t$ 的上界一般低于低估时对应的上界。 换句话说,低估带来的惩罚比高估大。因此如果使用 SMAPE 作为误差指标,其预测销量一般会高于实际销量。
4.3 MAAPE
Sungil Kim 和 Heeyoung Kim3 提出了一个有意思的误差指标 MAAPE,即 Mean Arctangent Absolute Percentage Error。与MAPE相比,它把 $p_t/100 = e_t/x_t$理解成直角三角形中的切角(见下图)。

因此 $\theta_t = \arctan(e_t/x_t)$。MAAPE即为 $\theta_t$ 的均值:
$$\text{MAAPE} = \frac{1}{n}\sum_{t=1}^n \theta_t.$$
优点
- 始终可计算。
- MAAPE有界,即:$0 \leq \text{MAAPE} \leq \frac{\pi}{2}$。
- 有较好的可解释性。
缺点
- 如果用MAAPE作为误差指标,其预测销量一般会低于实际销量。可以验证:低估时 $\theta_t$ 的上界为 $\pi/4$,而高估时对应的上界为 $\pi/2$。
5. 误差指标汇比较结果汇总
绝对误差
| 误差指标 | 中文 | 优点 | 缺点 | 说明 |
|---|---|---|---|---|
| MAE | (算术)平均绝对误差 | 直观 | 对异常值敏感 | 需要确认预测的目标与误差指标是否一致 |
| GMAE | 几何平均绝对误差 | 对异常值不敏感 | 1. $e_t\neq 0$; 2. 计算相对耗时 | 需要确认预测的目标与误差指标是否一致 |
| RMSE | 根均方误差 | - | 对异常值非常敏感 | 需要确认基本假设(例如误差是正态分布) |
绝对百分比误差
| 误差指标 | 中文 | 优点 | 缺点 | 说明 |
|---|---|---|---|---|
| MAPE | 平均百分比绝对误差 | 直观/容易计算 | 1. 对异常值敏感; 2. $x_t\neq 0$; 3. 预测值偏小 | 不推荐使用 |
| SMAPE | 对称的平均绝对百分比误差 | 1. 始终可计算; 2.形式上对称 | 1. 实际中预测值偏大; 2. 解释性差 | 需要确认预测的目标与误差指标是否一致 |
| MAAPE | 平均反正切绝对百分比误差 | 1. 始终可计算; 2. 有一定的解释性 | 预测值偏小 | 需要确认预测的目标与误差指标是否一致 |
说明
- 在实际中我们不能盲目地使用已知的误差指标,也不存在"万金油"的误差指标。我们采用(设计)的误差指标必须与业务目标一致。即,误差指标的提升会带来业务目标的提升。
- 使用百分比误差时,必须注意误差指标会引发预测销量比实际销量偏小或者偏大的风险。
6. 示例
我们用一个简单的例子来说明百分比误差引起的预测值偏大或偏小的问题。
例 假设 $n=1000$,实际销量为 1-100 的均匀分布,即 $x_t=t \mod 100$,其中 $t=1, 2, \ldots, n$ (若 $x_t=0$,令 $x_t=100$)。我们的预测模型为 $y_t=k$ ($k$ 为 1-100 之间的整数)。
下面考虑三种误差指标 MAPE, SMAPE 和 MAAPE。它们对应的最优预测结果如下图所示。
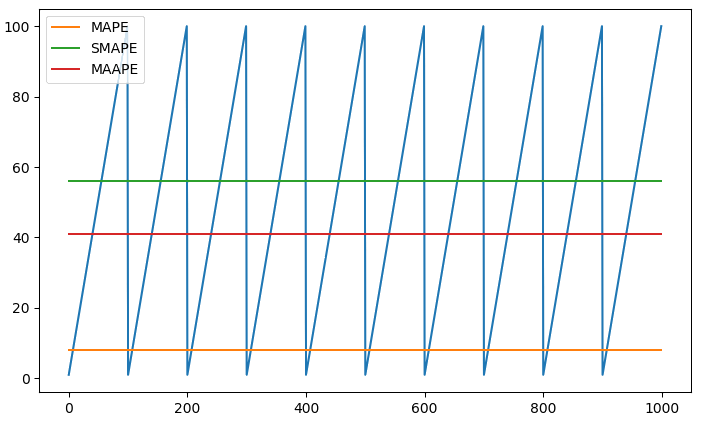
| 误差指标 | 最优 k 值 | 误差值 | 结论 |
|---|---|---|---|
| MAPE | 8 | 85.99 | 严重偏低(销量的均值为 50.5) |
| SMAPE | 56 | 56.33 | 偏高 |
| MAAPE | 41 | 0.5272 | 偏低 |
警告 MAPE 是业界使用最多的误差指标, 其预测模型产生的预测结果会明显偏低, 因此我们在使用中一定要确认预测目标与误差指标的一致性!
7. 总结
- RMSE 经常作为预测模型的误差指标(损失函数),其理论依据是建立在误差满足正态分布的假设下。首先我们要验证用于拟合的样本是否满足该条件。其次,RMSE 对异常值敏感,为了获得稳定的效果,我们一般需要对数据做一些平滑处理。
- 百分比误差 MAPE (以及类似的变种) 是被滥用的误差指标。如果你正在使用,请确保业务方了解该误差指标带来的风险。
- 没有万金油的误差指标,应该根据自己实际的业务目标来确定销量预测的误差指标。一个基本原则是确定误差指标的提升能带来业务的提升。
- 尽量不要使用单一的目标来衡量预测效果。
- 尽量不要使用单一的预测结果去支持多种业务。
参考文献
S. Makridakis and M. Hibon. The m3-competition: Results, conclusions and implications. International Journal of Forecasting, 16:451-476, 2000. ↩︎
IJCAI’ 17 Competition. https://tianchi.aliyun.com/competition/information.htm?spm=5176.100067.5678.2.2f6f5933auxKS4&raceId=231591&_lang=zh_CN ↩︎
Sungil Kim and Heeyoung Kim. A new metric of absolute percentage error for intermit- tent demand forecasts. International Journal of Forecasting, 32:669-679, 2016. ↩︎